매니커 알고리즘(Manachar's Algorithm)

Posted May 25, 2024

By Youjin Lee 16 min read

[1] 개요

Manachar’s 알고리즘은 주어진 문자열 내에서 가장 긴 Palindrome 부분 문자열을 찾는 알고리즘이다. Panlindromic한 문자열 혹은 Palindrome은 정방향으로 읽던 역방향으로 읽던 똑같은 문자열을 의미한다(e.g. abba, abcba).

Palindrome의 특성

palindrome은 중심에서 왼쪽과 오른쪽의 문자 배열이 대칭을 이룬다는 특성이 있다. 중심이 존재하기 위해서는 palindrome의 길이가 홀수여야 하기 때문에 Manachar 알고리즘에서는 문자열에 dummy 문자를 끼워넣는 전처리가 필요하다. 이 간단한 특성을 이용해서 중복 계산을 줄여 시간 복잡도에서 이점을 취한다. Brute Force로는 O(n^2) 혹은 O(n^3)에 풀리는 문제를 O(n)에 해결할 수 있다. 시간 복잡도에 대해서는 알고리즘 구현 후 아래에서 자세히 이야기할 예정이다.

Manachar 알고리즘 동작 방식

주어진 문자열이 xabay라고 할 때, dummy 문자를 끼워넣어 #x#a#b#a#y#로 만들어준다. 각 문자를 순회하면서 그 문자를 중심으로 하는 palindrome의 반지름을 저장한다. 반지름은 palindrome 길이의 절반을 의미하며 중심에서 palindrome의 마지막 문자까지의 거리이다. 결과는 P[0, 1, 0, 1, 0, 3, 0, 1, 0, 1, 0]이 된다.

여기서 알 수 있는 점

결과 배열 P가 최댓값을 기준으로 대칭을 이룬다. 모든 경우에 대칭을 이룰까? 그건 아니다. 여러 palindrome이 겹쳐져 있는 경우에 P는 대칭을 이루지 않는다. (예: #a#b#a#a#b# -> P[0, 1, 0, 3, 0, 1, 4, 1, 0, 1, 0])
P[5]에서 3으로 최댓값을 가지고, 이는 원래 문자열 xabay에서 최대 palindrome의 길이가 된다. 지름이 아닌 반지름을 저장하는 이유는 여기에 있다. palindrome이 대칭을 이루기 때문에 전체 길이를 알 필요가 없고, dummy 문자열을 끼워 넣어 이미 사이즈가 2N+1로 커졌기 때문에 반지름 값은 원래 문자열에서 palindrome의 길이를 나타내기 때문이다.

[2] Manachar’s Algorithm

// 변수 정의
S: 주어진 문자열에 dummy 문자 `#`을 끼워 넣어 새로 만든 문자열  
P: i번째에서의 palindrome의 반지름 길이
(🔴빨간색은 새로 읽은 값, 🟢초록색은 대칭성을 이용해 기존의 값을 가져온 값)  
C: 현재 유효한 palindrome의 중심 인덱스  
R: 현재 유효한 palindrome의 마지막 인덱스  

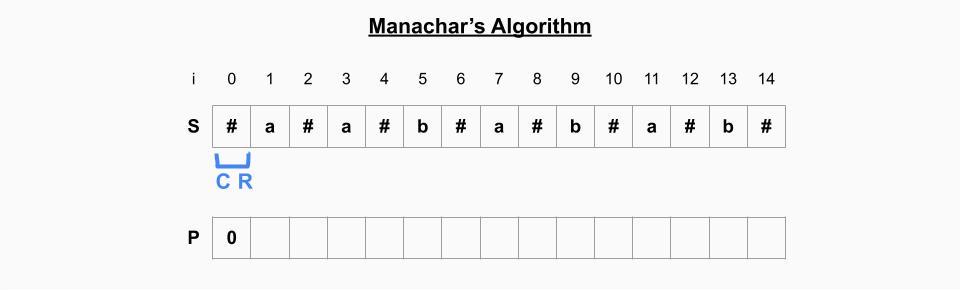
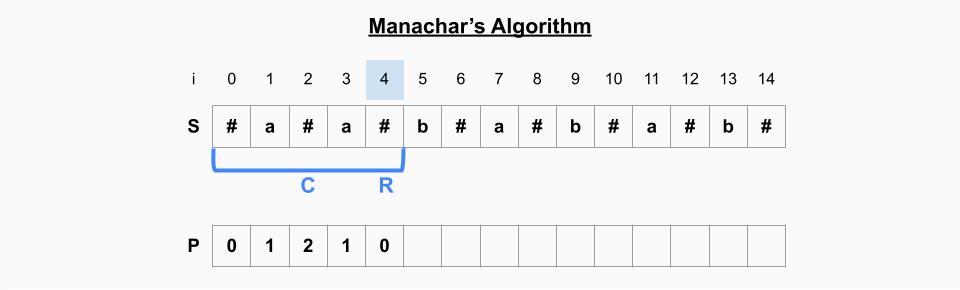
초기화

왼쪽 값이 없기 때문에 palindrome이 될 수 없어 항상 P[0]=0이다.
C=0, R=0

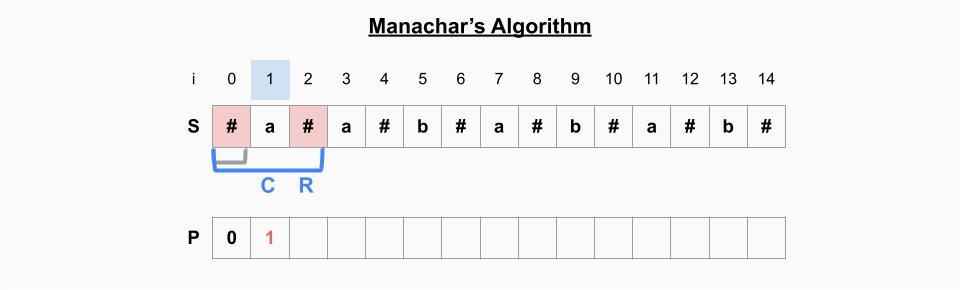
i=1일 때

i가 기존의 palindrome 범위(회색 괄호)을 벗어나기 때문에 새로 연산을 한다. -> S[2]=S[0]으로 P[1]=1
현재의 palindrome의 가장 오른쪽 인덱스(i=2)가 기존 palindrome의 가장 오른쪽 인덱스(i=0)보다 크기 때문에 새로 palindrome 범위를 업데이트 해준다. -> C=1, R=2

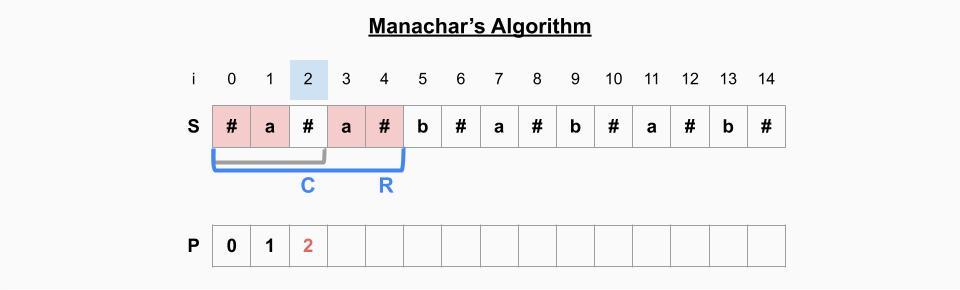
i=2일 때

i가 기존의 palindrome 범위(회색 괄호)안에는 있지만 범위의 가장 오른쪽에 위치해있어 i=2 기준으로 오른쪽에 대한 정보가 아직 없으므로 새로 연산을 해야한다. -> S[3]=S[1], S[4]=S[0]으로 P[2]=2
현재의 palindrome의 가장 오른쪽 인덱스(i=4)가 기존 palindrome의 가장 오른쪽 인덱스(i=2)보다 크기 때문에 새로 palindrome 범위를 업데이트 해준다. -> C=2, R=4

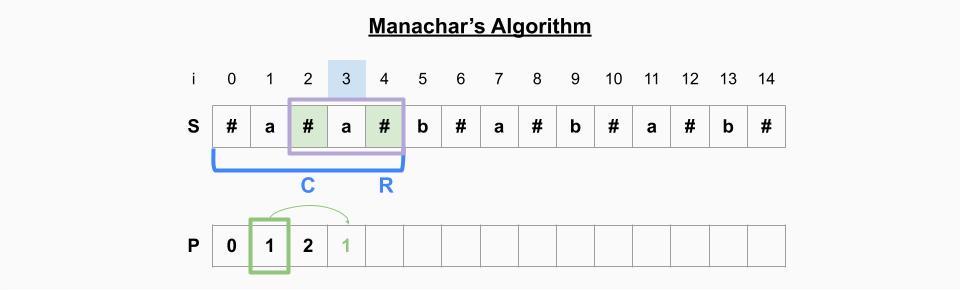
i=3일 때

i는 기존의 palindrome 범위 안에 안전히 위치해 있어 기존의 정보를 사용할 수 있다. 기존 palindrome의 중심 C를 기준으로 P[3]의 미러링 원소 P[1]의 값을 가져올 수 있는데, 이 때 P[3]=P[1]을 취했을 때 여전히 기존의 palindrome 범위 안에 있는지 확인해야한다. 범위 안에 있으므로 P[3]=1이 된다. 만약 범위를 벗어난다면 벗어나지 않을 만큼만 취해야한다.
P[5]!=P[1] 이기 때문에 더 이상 양 옆으로 expand하지 않는다.
palindrome의 오른쪽 인덱스가 i=4, 기존 palindrome의 오른쪽 인덱스가 i=4로 같기 때문에 범위를 업데이트 하지 않는다.

i=4일 때

범위 내 가장 오른쪽 인덱스이기 때문에 새로 연산을 한다. -> P[5]!=P[3]이기 때문에 P[4]=0
palindrome의 오른쪽 인덱스가 i=4, 기존 palindrome의 오른쪽 인덱스가 i=4로 같기 때문에 범위를 업데이트 하지 않는다.

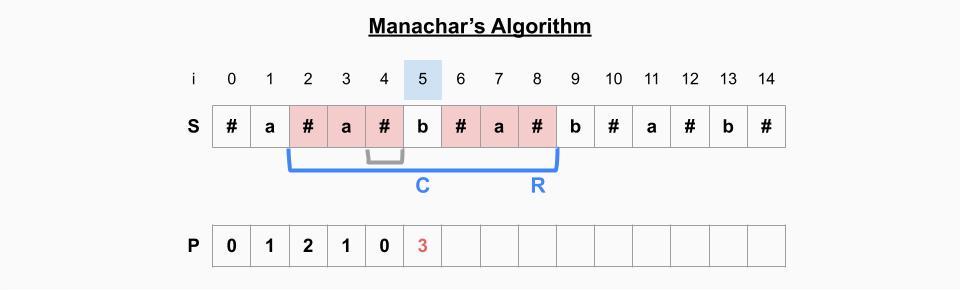
i=5일 때

i가 기존의 palindrome 범위(회색 괄호)을 벗어나기 때문에 새로 연산을 한다. -> P[6]=P[4], P[7]=[3], P[8]=P[2]로 P[5]=3
현재의 palindrome의 가장 오른쪽 인덱스(8)가 기존 palindrome의 가장 오른쪽 인덱스(4)보다 크기 때문에 새로 palindrome 범위를 업데이트해준다. -> C=5, R=8

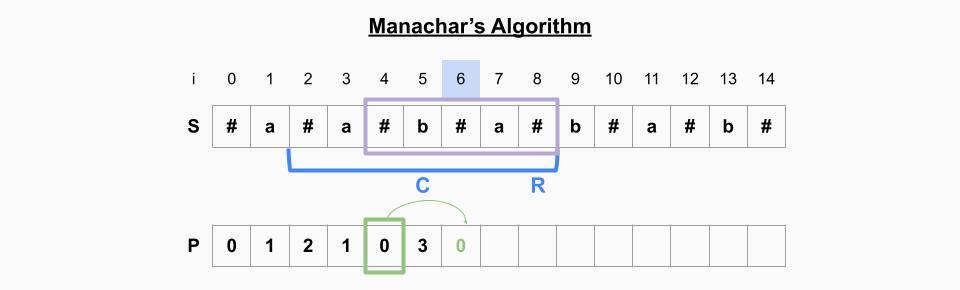
i=6일 때

P[6]의 미러링 원소 P[4]의 값을 취해도 여전히 범위 안에 있다. -> P[6]=P[4]=0
P[7]!=P[5]이기 때문에 더 이상 양 옆으로 expand하지 않는다.
현재 palindrome의 오른쪽 인덱스(6)이 기존 palindrome의 오른쪽 인덱스(8)보다 작기 때문에 범위를 업데이트 하지 않는다.

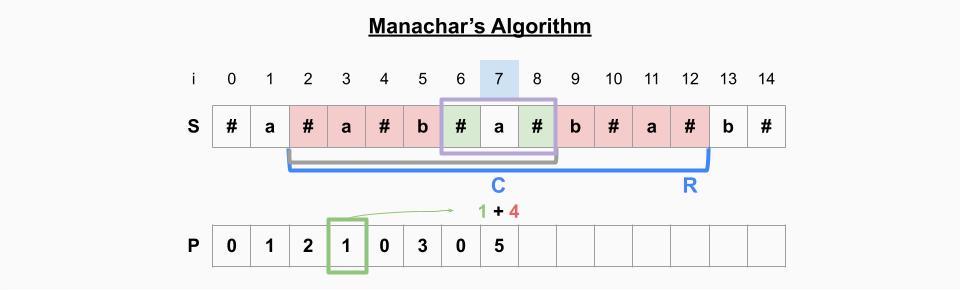
i=7일 때

P[7]의 미러링 원소 P[3]=1의 값을 취해도 기존 palindrome(회색 괄호)를 벗어나지 않는다. -> 우선 P[7]=P[3]=1
P[9]=P[5], P[10]=[4], P[11]=P[3], P[12]=P[2]이므로 4를 더해준다. -> P[7]=1+4=5
현재 palindrome의 오른쪽 인덱스(12)가 기존 palindrome의 오른쪽 인덱스(8)보다 크기 때문에 범위를 업데이트 한다. -> C=7, R=12

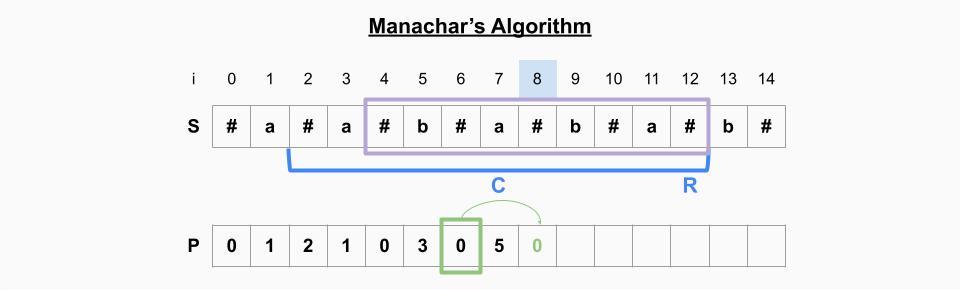
i=8일 때

P[8]의 미러링 원소 P[6]의 값을 취해도 여전히 범위 안에 있다. -> P[8]=P[6]=0
범위는 업데이트 하지 않는다.

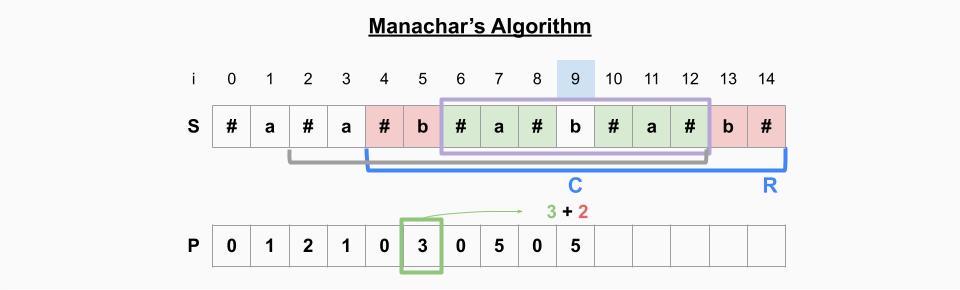
i=9일 때

P[9]의 미러링 원소 P[5]의 값을 취해도 여전히 범위 안에 있다. -> 우선 P[9]=P[5]=3
P[13]=P[5], P[14]=[4]이므로 2를 더해준다. -> P[9]=3+2=5
현재 palindrome의 오른쪽 인덱스(14)가 기존 palindrome의 오른쪽 인덱스(12)보다 크기 때문에 범위를 업데이트 한다. -> C=9, R=14

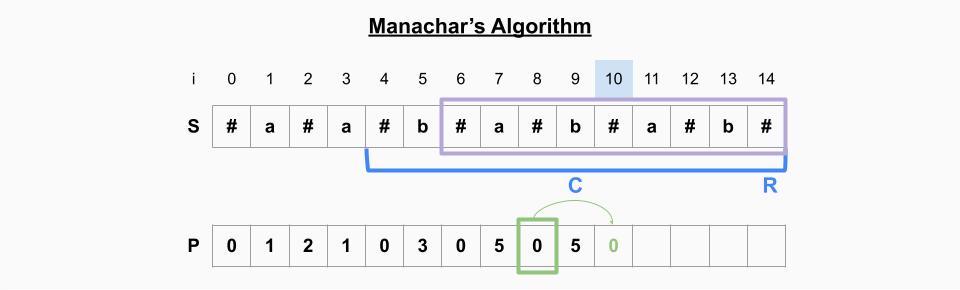
i=10일 때

P[10]의 미러링 원소 P[8]의 값을 취해도 여전히 범위 안에 있다. -> P[10]=P[8]=0
P[11]!=P[9]이기 때문에 더 이상 양 옆으로 expand하지 않는다.
현재 palindrome의 오른쪽 인덱스(10)이 기존 palindrome의 오른쪽 인덱스(14)보다 작기 때문에 범위를 업데이트 하지 않는다.

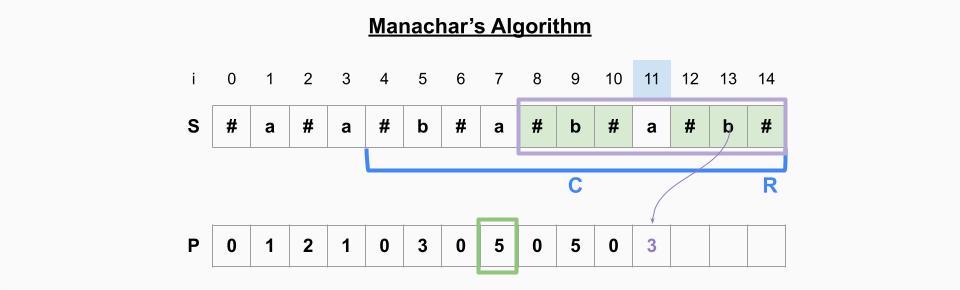
i=11일 때

P[11]의 미러링 원소 P[7]을 취하면 기존 palindrome의 범위(파란 괄호)를 벗어난다. 범위를 벗어나지 않는 한도 내에서 선택한다. -> P[11]=3
현재 palindrome의 오른쪽 인덱스(11)이 기존 palindrome의 오른쪽 인덱스(14)보다 작기 때문에 범위를 업데이트 하지 않는다.

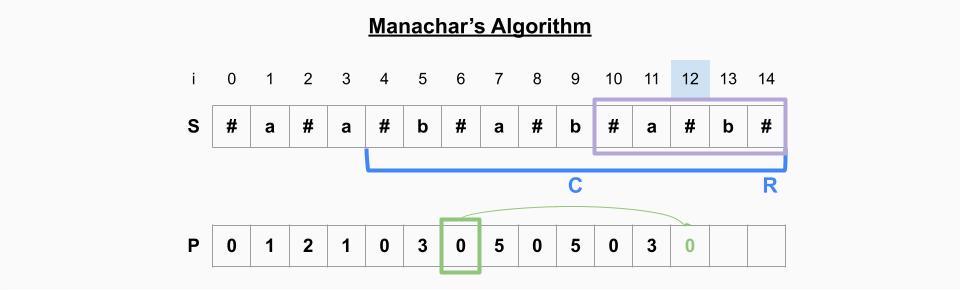
i=12일 때

P[12]의 미러링 원소 P[6]의 값을 취해도 여전히 범위 안에 있다. -> P[12]=P[6]=0
현재 palindrome의 오른쪽 인덱스(12)이 기존 palindrome의 오른쪽 인덱스(14)보다 작기 때문에 범위를 업데이트 하지 않는다.

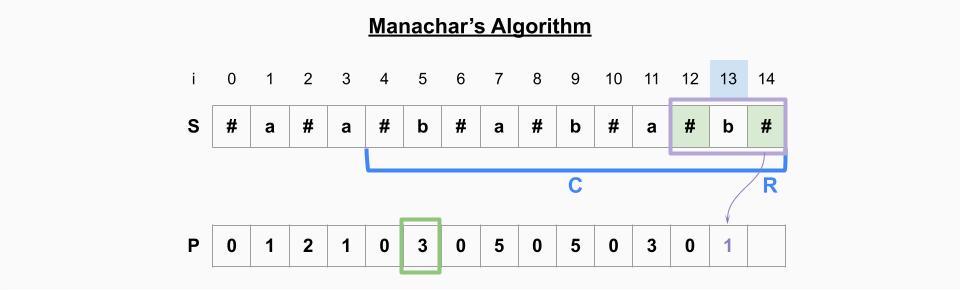
i=13일 때

P[13]의 미러링 원소 P[5]을 취하면 기존 palindrome의 범위(파란 괄호)를 벗어난다. 범위를 벗어나지 않는 한도 내에서 선택한다. -> P[13]=1
현재 palindrome의 오른쪽 인덱스(13)이 기존 palindrome의 오른쪽 인덱스(14)보다 작기 때문에 범위를 업데이트 하지 않는다.

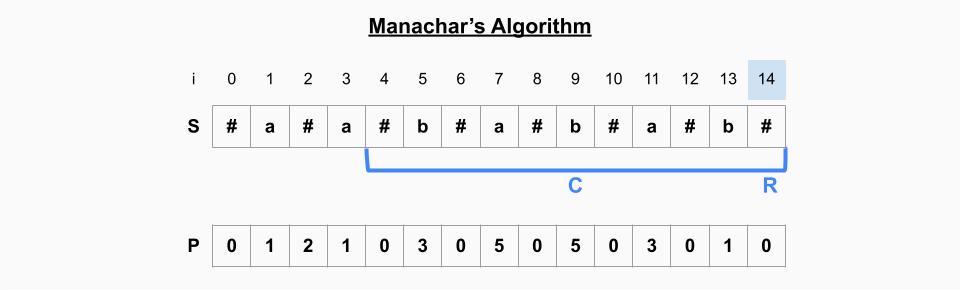
i=14일 때

배열의 마지막 원소라서 오른쪽에 대한 정보가 없기 때문에 항상 0이다. -> P[14]=0
현재 palindrome의 오른쪽 인덱스(14)이 기존 palindrome의 오른쪽 인덱스(14)보다 크지 않기 때문에 범위를 업데이트 하지 않는다.

결과

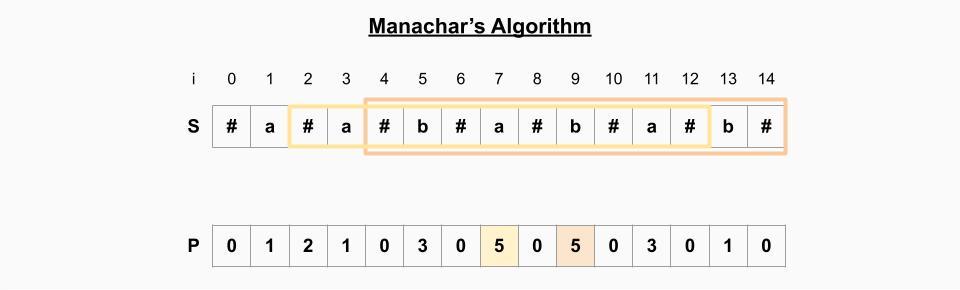배열 P에서 최댓값을 구한다. i=7, i=9일 때 최댓값 P[7]=P[9]=5가 된다. 그 최댓값을 반지름으로 갖는 palindrome을 구한다. 각각 ababa, babab가 된다.

[3] 구현

Leetcode 5번 Longest Palindromic Substring

  
func longestPalindrome(s string) string {
	if len(s) == 1 {
		return s
	}
	S := "#" + strings.Join(strings.Split(s, ""), "#") + "#"
	P := make([]int, len(S))
	C, R := 0, 0

	for i := 1; i < len(S); i++ { // i=1부터 순회
		if i < R { // i가 기존 palindrome 범위에 안전히 존재하면
			P[i] = min(R-i, P[2*C-i]) // 기존 palindrome 범위 내에 존재할 것을 보장하는 미러링 원소의 값을 택한다.
		}
		for i+P[i] < len(S)-1 && i-P[i] >= 1 && // 배열 밖을 벗어나지 않고
        S[i+P[i]+1] == S[i-1-P[i]] { // 양 옆으로 expand해서 같은 값을 가지면
			P[i]++ // P[i]에 1을 더해준다.
		}
		if i+P[i] > R { // 현재 i를 기준으로 하는 palindrome의 오른쪽이 기존 palindrome의 오른쪽 인덱스보다 크면
			C, R = i, i+P[i] // palindrome 범위를 새로 업데이트 한다.
		}
	}

	max := 0
	maxIndex := 0
	for i, v := range P {
		if v > max {
			max = v
			maxIndex = i
		}
	}

	return s[(maxIndex-max)/2 : (maxIndex+max)/2]
}

func min(a int, b int) int {
    if a < b {
        return a
    } else {
        return b
    }
}

[4] 시간복잡도

얼핏보면 nested loop 때문에 O(n^2)인 것 같아 보이지만 그렇지 않다. 결론부터 말하자면 O(N)+O(N)=O(N)이다.

우선, outer loop가 S 배열을 차례로 순회하는데 S 배열의 크기가 2N+1이기 때문에 O(N)이다. inner loop에서는 양쪽의 수가 다를 때까지 양옆으로 expand하는데, 미러링 원소를 통해 얻은 값으로 S배열을 중복해서 읽을 필요가 없기 때문에 모든 연산을 마칠 때까지 배열의 원소를 딱 한 번씩만 읽는다. 위의 알고리즘 동작 방식 이미지를 i=1부터 i=14까지 쭉 훑어보면서 i를 기준으로 오른쪽에 새로 읽는 값(S 배열의 빨간색)이 중복되는지 확인해보면 쉽게 알 수 있다. i=1일 때 P[2], i=2일 때 P[3], P[4], i=5일 때 P[6], P[7], P[8]…(생략)

매번 outer loop를 순회할 때마다 inner loop가 N번씩 순회하는 것이 아니라 outer loop의 순회를 시작하고 마칠 때까지 inner loop의 축적된 연산이 총 O(N)이기 때문에 O(N)*O(N)=O(N^2)가 아닌 O(N)+O(N)=O(N)이 되는 것이다.

[5] 공간복잡도

palindrome의 반지름을 저장할 P 배열을 사용했다. 공간복잡도는 O(2N+1)=O(N)이다.

[6] 결론

Manachar’s 알고리즘은 palindrome의 대칭성을 이용하여 중복된 계산을 줄여 O(N) 시간 안에 가장 긴 palindrome을 찾는 알고리즘이다. 구현된 코드를 먼저 보면 R-i 혹은 2*C-i 등 무엇을 의미하는지 알기 어렵기 때문에 그림으로 알고리즘을 먼저 익히는 편이 이해하기 쉽다. dummy 문자를 끼워 넣는 이유, 지름이 아닌 반지름을 저장하는 이유 등 공부하면서 의문이 생겼던 부분도 같이 정리해보았다. 특히 시간복잡도를 이해하는 데 시간을 많이 썼지만 이제는 자신 있게 O(N)이라고 말할 수 있게 되었다.

Computer-Science, Algorithm

algorithm

This post is licensed under CC BY 4.0 by the author.