플로이드 순환 검출 알고리즘(Floyd's Cycle Detection Algorithm)

a.k.a 토끼와 거북이 알고리즘(Tortoise🐢 & Hare🐇 Algorithm) / Slow & Fast Algorithm

[1] 개요

• 플로이드 순환 검출 알고리즘은 토끼와 거북이 알고리즘 혹은 Slow&Fast 알고리즘이라고도 불린다.
• 속도를 달리하는 두 개의 포인터를 가지고 순환 구간이 존재하는지, 존재한다면 순환 구간이 어느 노드에서 시작하는지 검출할 수 있다.

[2] 동작 방식

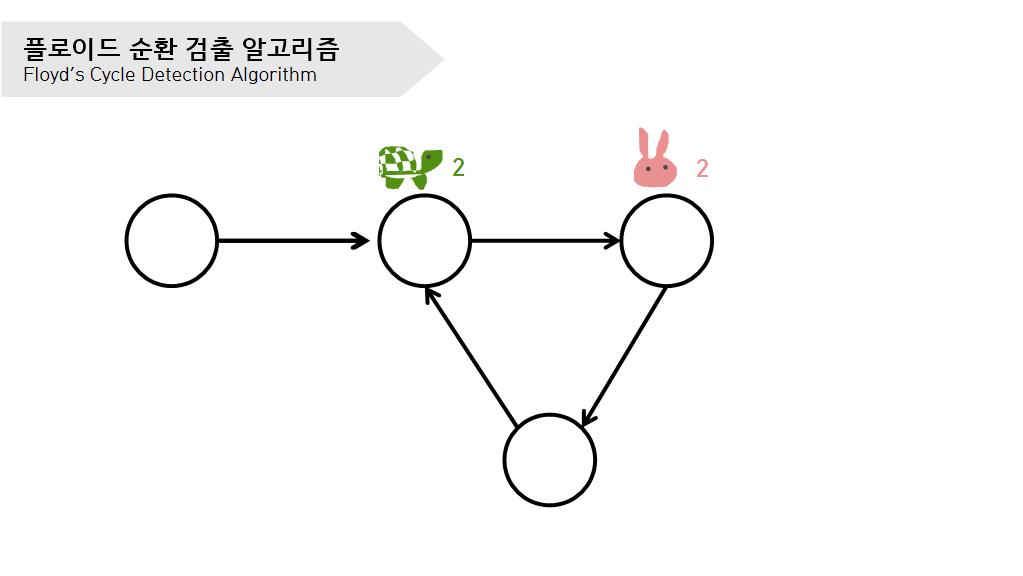
1. 거북이는 1칸씩, 토끼는 2칸씩 움직인다.
2. 거북이와 토끼가 만나면 거북이를 출발 지점으로 옮긴다.
3. 거북이와 토끼를 각각 1칸씩 옮긴다.
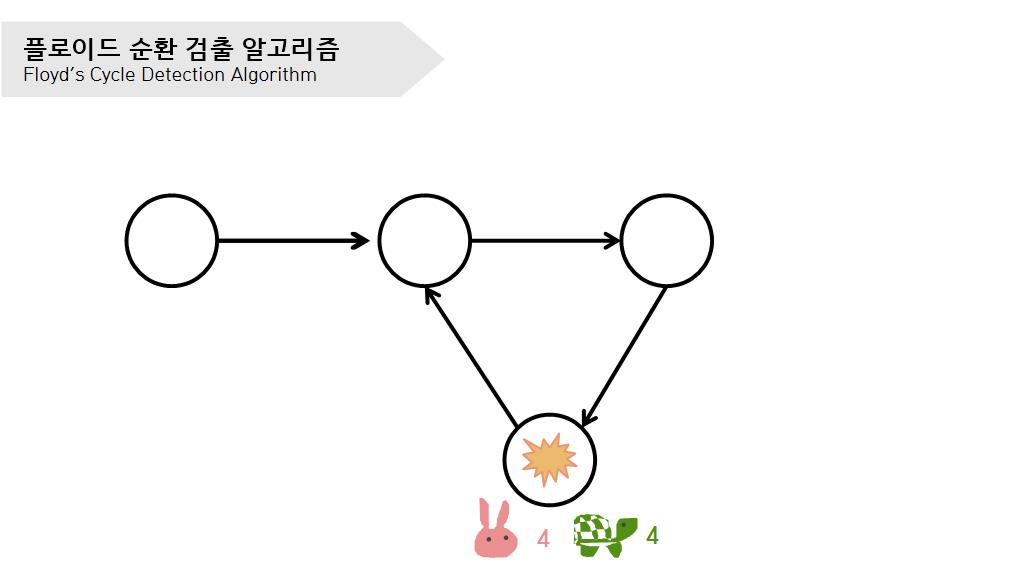
4. 거북이와 토끼가 다시 만난다.

발로 그린 거북이와 토끼를 준비하고 그림으로 표현해보았다.

우선 거북이와 토끼가 만날 때까지 거북이는 1칸, 토끼는 2칸씩 움직인다.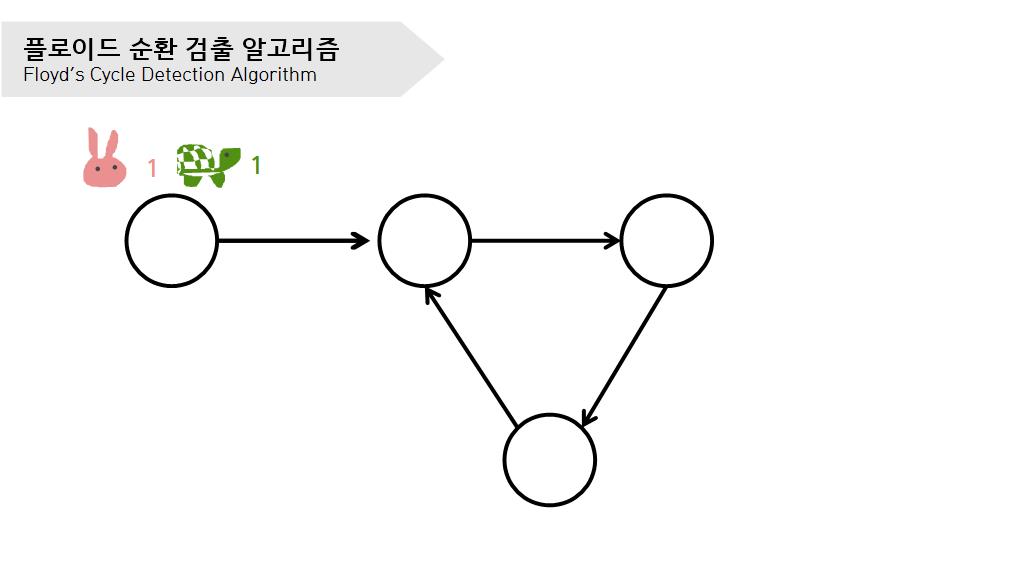

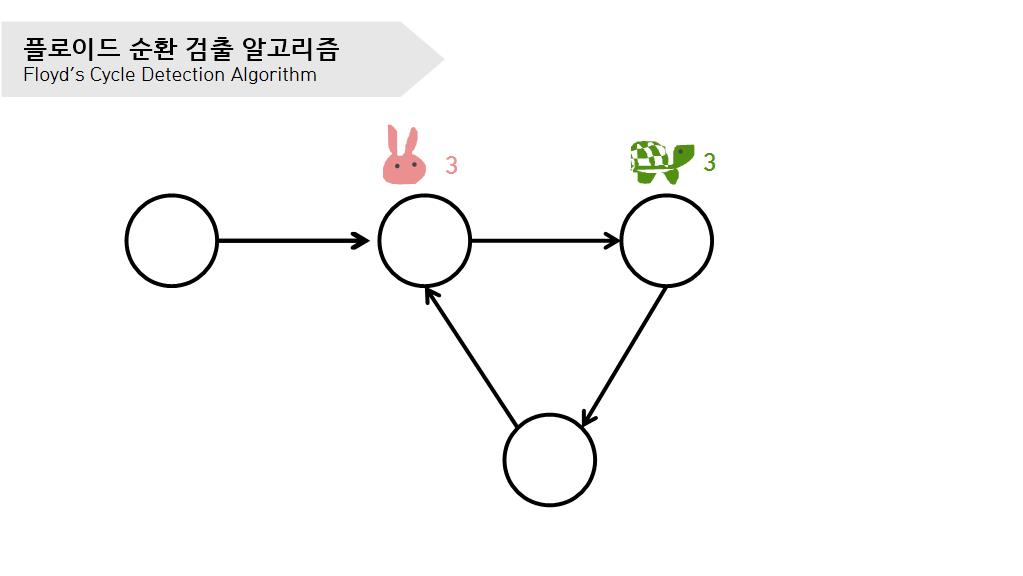
거북이와 토끼가 만났으면 거북이를 출발 지점으로 옮긴다.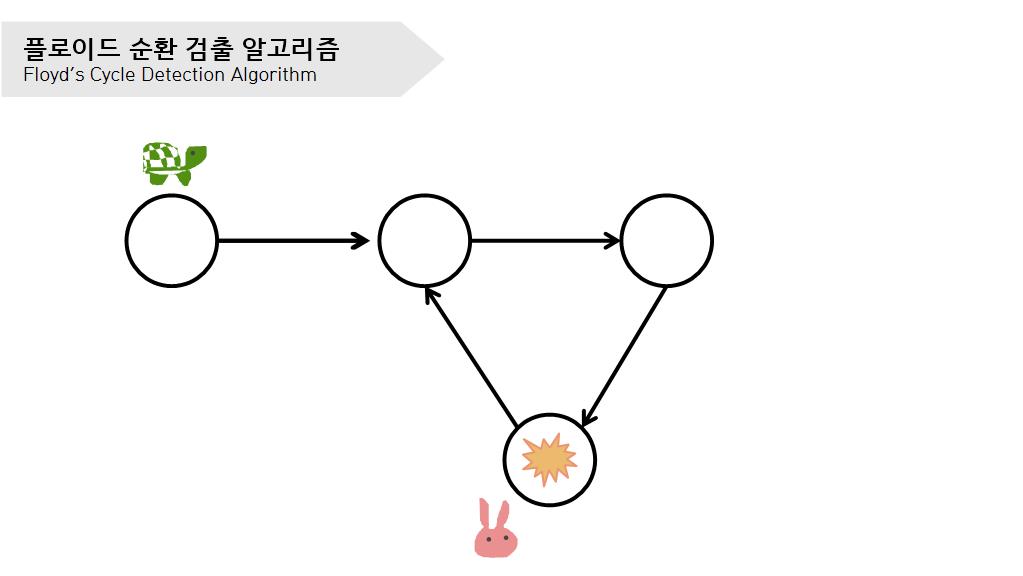

거북이와 토끼가 다시 만날 때까지 거북이도 1칸, 토끼도 1칸씩 움직인다.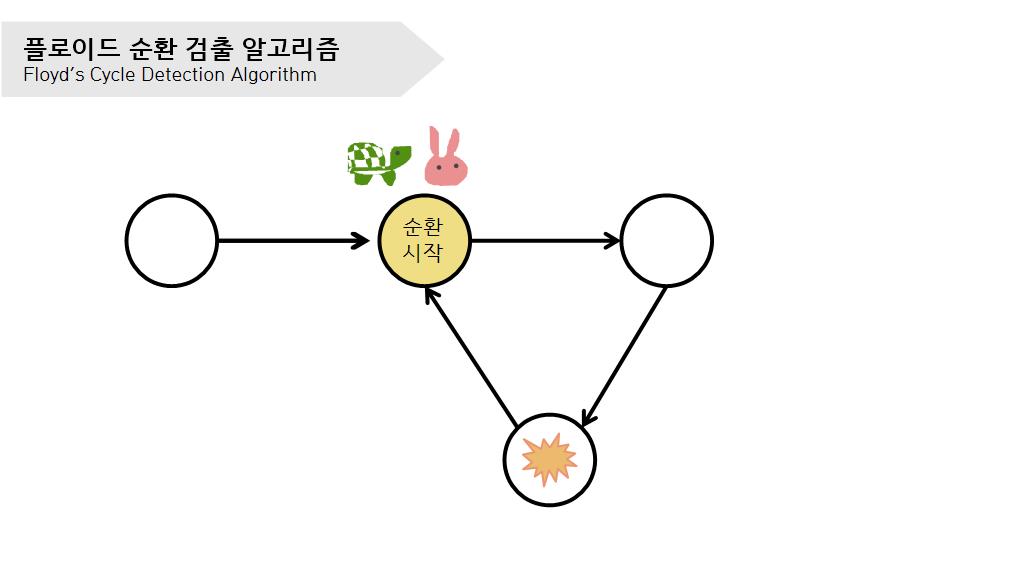

이 알고리즘에서 알 수 있는 것은 크게 두 가지이다.

• 거북이와 토끼가 만났다면 순환하는 구간이 존재한다.
• 거북이를 시작 지점으로 옮긴 후 거북이와 토끼가 다시 만나는 지점은 순환 구간이 시작하는 노드이다.

[3] 일반화

순환 구간이 존재하면 이동 거리와 위치가 비례하지 않아서 사실 제대로 증명하기가 좀 복잡한 것 같다. 명제1은 직관으로 이해할 수 있었지만 명제2는 따로 정리하기 전까지 받아들이기 힘들었다.

명제1

거북이와 토끼가 만났으면 순환하는 구간이 존재한다.
속력이 다른 두 사람이 달리기를 한다고 생각해본다. 이 때 속력은 빨라졌다 느렸졌다 하지 않고 일정하다고 가정한다. 직선트랙이라면 두 사람의 거리는 점점 멀어져 만날 수 없게 되겠지만 원형트랙이라면 둘은 만나게 될 것이다.

명제2

출발 지점에서부터 순환 구간이 시작하는 지점까지의 거리는 거북이와 토끼가 만난 지점에서부터 순환 구간이 시작하는 지점까지의 거리와 같다.(= 거북이와 토끼가 다시 만나는 지점은 순환 구간의 시작 지점이다.)

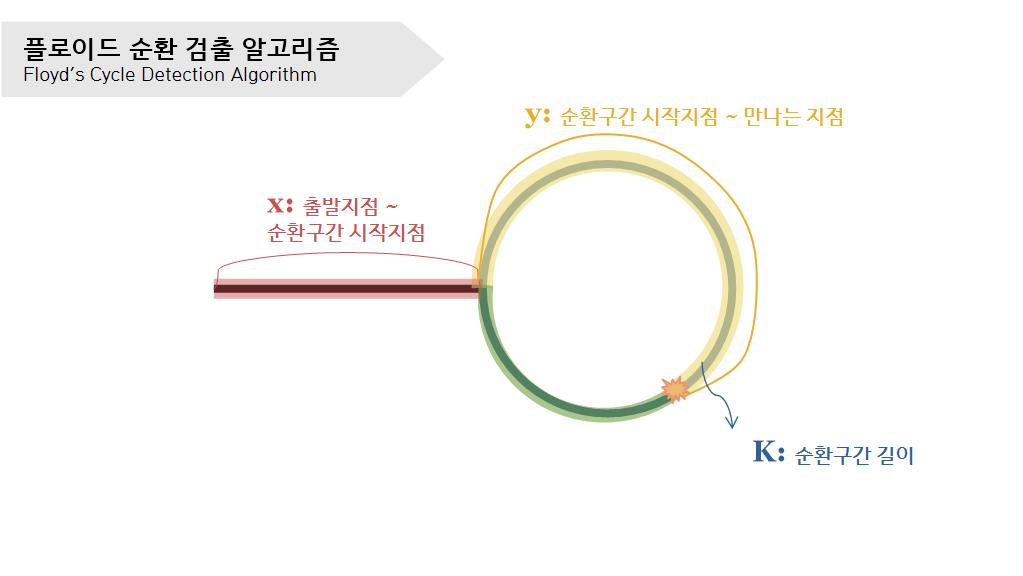
명제를 말로 풀어 설명하면 복잡해 보이지만 아래 사진에서 빨간 구간과 초록 구간의 길이가 같다는 것을 증명하면 된다.

• x: 출발 지점에서부터 순환 구간이 시작하는 지점까지의 거리
• y: 순환 구간이 시작하는 지점부터 거북이와 토끼가 만난 지점까지의 거리
• K: 순환 구간의 길이
• n1: 거북이가 이동한 순환 구간 바퀴 수
• n2: 토끼가 이동한 순환 구간 바퀴 수
• 토끼의 속력은 거북이의 속력의 2배이다.

1. 거북이가 이동한 거리는 x + K*n1 + y
2. 토끼가 이동한 거리는 x + K*n2 + y
3. 토끼는 거북이보다 2배 빠르기 때문에 2(x + K*n1 + y) = x + K*n2 + y
4. 식을 정리하면 x + y = (n2 - n1)K
5. n2 - n1은 상수이기 때문에 간략히 표현하면 x + y = N*K
6. 한번 더 정리하면 x = N*K - y이고 x는 N바퀴의 순환 길이에서 y를 뺀 것과 같다고 할 수 있고, 순환길이에서 y를 뺀 것은 위 사진의 초록 구간에 해당하기 때문에 명제는 성립한다고 볼 수 있다.

[4] 구현

🔽 순환 구간의 시작 지점을 구하는 Go 코드(Leetcode 142번 Linked List Cycle2)

/**
 * Definition for singly-linked list.
 * type ListNode struct {
 *     Val int
 *     Next *ListNode
 * }
 */
func detectCycle(head *ListNode) *ListNode {
    if head == nil {
        return nil
    }
    slow, fast := head, head // 거북이와 토끼

    // 순환 구간이 존재하는지 판단
    var hasCycle = false
    for fast.Next != nil && fast.Next.Next != nil {
        slow = slow.Next // 거북이는 한 칸씩 이동
        fast = fast.Next.Next // 토끼는 두 칸씩 이동
        if slow == fast { // 거북이와 토끼가 만났다면
            hasCycle = true // 순환 구간이 존재
            break
        }
    }
    
    // 순환 구간이 존재하지 않으면 nil 반환
    if !hasCycle {
        return nil
    }

    // 순환 구간이 존재한다면
    slow = head // 거북이를 출발 지점으로 이동
    for slow != fast { // 거북이와 토끼가 만날 때까지 한 칸씩 이동
        slow = slow.Next
        fast = fast.Next
    }
    return slow
}